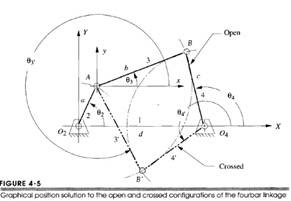
El mecanismo debe ser de 4 barras y se rige por las ecuaciones descritas en el libro “Diseño de maquinaria”de Robert L Norton.
El angulo de entrada tiene el siguiente rango:

Y la ecuación que buscamos que cumpla el angulo de salida es:

Graficando esto con ayuda de matlab tenemos
Lo que es esperado ya que el valor cuadrado es muy pequeño,
y resulta casi que el ángulo de salida es el contrario al de la entrada.
Se procedió en matlab:
La función punto1main.m consiste en evaluar, por medio de fmincon, la función
que deseamos optimizar que es punto1m4bar
y punto1m4bar2 esto porque es diferente
si tomamos el mecanismo como cruzado o como abierto
Ilustración 1 - Tomada de Diseño de maquinaria- Robert
Norton pg 175
Las funciones consisten en comparar, a través de las
formulas que permiten establecer el angulo de salida en función del angulo de
entrada y la longitud de las barras con la función dada.
Se incluye una instrucción para comprobar que el mecanismo
pueda ensamblarse, lo que se logra comprobando que no existen números complejos
dentro de la formula.
x(4)=1;
k1=x(4)/x(1);
k2=x(4)/x(3);
k3=(x(1)^2-x(2)^2+x(3)^2+x(4)^2)/(2*x(1)*x(3));
k4=x(4)/x(2);
k5=(x(3)^2-x(4)^2-x(1)^2-x(2)^2)/(2*x(1)*x(2));
se hace un barrido a través de el angulo de entrada dado con
un for, a la vez que se comprueban los complejos, se halla el angulo de
salida y se comprara con la función:
for teta=-0.349:0.001:0.349
A=cos(teta)-k1-(k2*cos(teta))+k3;
B=-2*sin(teta);
C=k1-((k2+1)*cos(teta))+k3;
D=cos(teta)-k1+k4*cos(teta)+k5;
E=-2*sin(teta);
F=k1+(k4-1)*cos(teta)+k5;
if (B^2-4*A*C)<=0 ||(E^2-4*D*F)<=0;
error1acum=error1acum+1e3*abs(B^2-4*A*C);
end
teta4=2*atan( (-B -sqrt(B^2-4*A*C)) / (2*A));
funcgalea=0.2865*teta^2-teta;
error1=abs(teta4-funcgalea);
error1acum=error1acum+error1;
f=error1acum;
este error acumulado es la suma de cada error puntual para
el barrido, siendo el error puntual llamado “error1” que es la diferencia
absoluta puntual entre la función dada y la función aproximada por el
mecanismo.
Cabe destacar el bloque if, donde se busca que la
optimización se “aleje” de los números complejos utilizando convenientemente
los valores absolutos de dichas raíces cuando son negativas, se toma su valor
absoluto, se multiplica por 1000, y se adiciona… asegurando que el programa se
aleje de este crecimiento repentino de la función. Esta restricción artificial
fue necesaria ya que no es la misma para diferentes valores de las barras y
ángulos, lo que dificulta la creación de una restricción desde la función
punto1main.m.
Como resultados tenemos:
Al ejecutar el programa, obtenemos los datos de las barras:
24.5621 0.0364 23.5882
y las graficas de comparación de las funciones y el error. Nótese la gran inexactitud que se presenta.
y las graficas de comparación de las funciones y el error. Nótese la gran inexactitud que se presenta.
Dicha inexactitud se
presenta por las complicaciones en el rango de el angulo de entrada, que hacen
que el angulo de salida sea imposible de conseguir. El movimiento necesitado es
similar a dos engranajes, que resulta imposible su transporte a un mecanismo de
4 barras.
Lo mas cercano, es la construcción del mecanismo en un ángulo diferente, o en
un rango sin que pasen por cero y se agarrote el mecanismo.
Ilustración 2 - yourdictionary.com
Se toman como variables la longitud de las 4 barras, la
distancia y ángulo del punto de acción del mecanismo (P), y adicionalmente un
ángulo y un desfase del ángulo donde se espera aproximar la distancia del punto
P a una función dada.
a)
En este caso, la función dada se evaluó como un polinomio de grado 5.
Fpunto2 utiliza esta función comparándola con la posición en X y en Y que
surgen a partir del ángulo de entrada. Es por esto que el ángulo de entrada
tuvo que ser definido como un rango especificado por x(7) y x(8).
Para aproximar la función entonces, se comparo el valor del
polinomio con el valor dado por el mecanismo. A esto se le saca valor absoluto
y se suma a lo largo del barrido angular.
px=x(1)*cos(teta)+x(5)*cos(teta3+x(6));
py=x(1)*sin(teta)+x(5)*sin(teta3+x(6));
py2=polyval(p,px);
f2=abs(py2-py);
f=f+f2
;
adicionalmente, se comprueba si hay números complejos lo que
impedirían el ensamble del mecanismo
if (B^2-4*A*C)<=0 ||(E^2-4*D*F)<=0 ;
error=1;
end
cuando error=1,
if error==1
f=1e6;
end
lo que asegura que el programa seguirá iterando alejándose
de los valores complejos.
Adicionalmente
a través del contador “iter” se trazó la convergencia definida como la función
que estamos minimizando para cada iteración
Se destacan los valores de 10^6 que son cuando se crearon
números complejos y el programa abandona dicha ruta de optimización.
Nuevamente
a través de “mecanismo4barras.m” se grafica el mecanismo girando en el rango
angular que fue optimizado, en la posición cruzada y abierta
En Excel, solver fue incapaz de hallar una
solución a pesar de multiples métodos para corregir las raíces de números
negativos y de utilizar posibles barridos angulares dada la misma dificultad de
encontrar los pares de números, en 5 ocasiones distintas
En gris: barras
En
gris a la derecha: ayuda para evitar raíces negativas,
en verde: celda objetivo
fue posible establecer el error como la diferencia entre
la posición X del mecanismo y 20, con resultados optimos
px=x(1)*cos(teta)+x(5)*cos(teta3+x(6));
f2=abs(px-20);
f=f+f2;
de esta manera el error fue fácil de optimizar en el rango
dado, que es escogido también por la maquina, o por las condiciones de frontera
establecidas